Ta dina bilder med universell harmoni

Det gyllene förhållandet upprepar sig i oändlighet, om och om igen. Vi kan titta på getters horn, kristaller, virvlar, fingeravtryck, spiral-armar hos galaxer eller på skalet hos en vanlig snigel. Och på något vis verkar tycke och smak för vad som är harmoniskt och vackert vara bestämt av naturen redan från början.

Men vad är det då som är så magiskt? Svaret är det som vi kallar för gyllene snittet. Uttrycket har på senare tid blivit kopplat till både mystik, religion och matematik. Och det är just ur matematiken som det gyllene snittet härstammar (läs faktarutan på nästa sida). Gyllene snittet utgår nämligen från vissa tal och den följd de har – något som gemensamt kallas för Fibonnachi-talen – som tillsammans har ett speciellt förhållande till varandra.

Tittar vi på de så kallade Fibonnachi-talen där en följd av tal byggs upp genom att nästkommande tal är summan av de två föregående, alltså 1, 1, 2, 3, 5, 8, 13 och så vidare – ser vi att ett speciellt förhållande börjar framträda: 5 förhåller sig till 3 (5:3) ungefär som 8 förhåller sig till 5 (8:5) och i sin tur ungefär som 13:8 och 21:13 och så vidare. Ju högre siffror vi använder desto närmare kommer vi talet 1,618 – det gyllene talet med oändliga decimaler som representerar det gyllene snittet och dess förhållande 1,618:1.

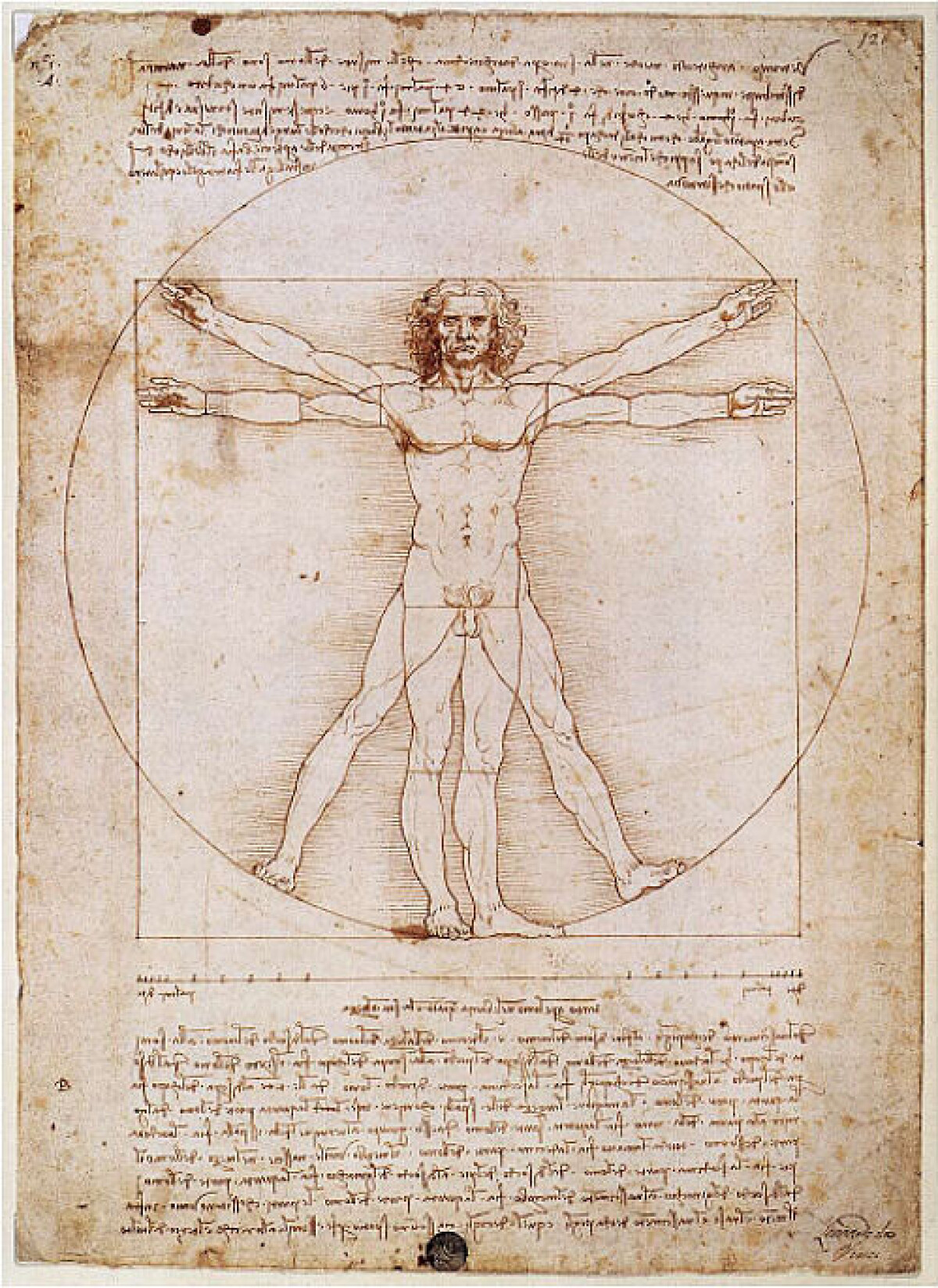
Trots en massa svårbegriplig matematik så återfinns dessa siffror i det som är oss närmast – på vår egen kropp. Längden mellan fötterna och huvudet förhåller sig till längden mellan naveln och fötterna med gyllene snittets förhållande. För huvudets hela längd och längden mellan ögonen och hakan gäller samma sak. Ett ansikte som bygger på dessa proportioner uppfattas alltså mer harmoniskt.

Där allt möts

Detsamma gäller när vi tittar på bilder. Vi kan dela upp en bild efter gyllene snittets förhållande på flera olika sätt. Bland annat kan vi rita en gyllene rektangel, som i sin tur kan bilda en gyllene spiral. Men det finns också gyllene trianglar och vinklar. Och allt växer fram från gyllene snittets förhållande 1,618.

När vi tittar på en bild kan vi använda förhållandet för att rita upp både vertikala och horisontella linjer. På så vis uppstår skärningspunkter där linjerna möts. Själva kärnan i resonemanget är att någonting ska hända i dessa skärningspunkter – ett objekt med betydelse ska befinna sig där, eller någon färg eller form som drar till sig uppmärksamhet ska placeras just där.

Samtidigt är de linjer som delar upp bilden i flera gyllene snitt också intressanta. Genom att placera horisonter, byggnader eller perspektivets djup i dessa linjer får vi harmoniska förhållanden mellan olika element i bilden.

Men det tar inte slut med linjer och skärningspunkter. Man kan gå ytterligare ett steg och blanda in gyllene trianglar och gyllene spiraler. Tittar vi exempelvis på en ormbunke som drar ihop sina blad så följer den formen av en gyllene spiral. Denna kurva kan vi sedan lägga över exempelvis en bild, och då vill vi att händelser i bilden ska placeras efter spiralkurvan för att få en viss dynamik, och bygga upp ett förhållande mellan objekt i bilden.

Tredjedelsregeln

På samma sätt som gyllene snittet fungerar det som kallas för tredjedelsregeln. Här är tanken att dela in bilden i nio lika stora delar med hjälp av två vertikala och två horisontella linjer. Sedan lyder regeln att du bör placera det du fotar i linjernas skärningspunkter, eller exempelvis horisonten längs med den nedre linjen.

Förhållandet med tredjedelsregeln kan uttryckas som 2:1, vilket också kan ses som de första siffrorna på vägen mot gyllene snittets förhållande 1,618. Få fotografer känner antagligen suget efter att exakt räkna ut detta förhållande samtidigt som de tar en bild – fågeln skulle flyga iväg, människan skulle somna och solen antagligen hinna gå ner – vilket innebär att tredjedelsregeln i stället fungerar som en bra fingervisning eller uppskattning om var gyllene snittets skärningspunkter befinner sig.

För oss människor upplevs ändå tredjedelsförhållandet likvärdigt med gyllene snittet. Som fotograf kan du därför tänka i tredjedelar, men få gyllene bilder.

Bryt reglerna

Eftersom du nu känner till två grundläggande och vanliga regler för att komponera bilder kan du utveckla ditt eget bildspråk genom att bryta dessa. Se snarare »reglerna« som en guide att utgå ifrån, där du sedan kan lägga till dina egna tankar och din egen känsla om vad som gör en bild bra. Vissa gånger kan en komposition som bryter helt mot gyllene snittet också vara den bästa för att framhäva det som händer.

Så börja med att gå ut och fota efter konstens alla regler och lär dig tala naturens eget språk med dina bilder. Leta efter intressanta mönster och gyllene förhållanden – då kommer dina bilder att bli ännu mer spännande när du väl vågar bryta mot denna universella harmoni.